AVL Tree 알고리즘
AVL Tree는 이진 검색 트리(Binary search Tree)의 한계를 극복하고자 고안된 자료구조입니다.
AVL은 이 자료구조를 만든 세 명의 이름(Adelson, Velskii, Landis) 에서 앞 글자를 딴 겁니다.
특징
AVL Tree는 이진 검색 트리이면서 동시에 균형을 유지하고 있습니다. 모든 노드의 왼쪽과 오른쪽 서브트리의 높이 차이가 1 이하입니다. 이렇게 균형을 유지하고 있기 때문에 이진 검색 시의 효율성을 보장할 수 있습니다. 균형이 갖추어진 이진 트리이기 때문에 완전 이진 트리(CBT)와 비슷한 형태를 보이게 됩니다.
최적의 검색 속도를 보장하기에 아주 효율적이고, 검색을 할 때 O(log n)에 해당하는 검색 속도를 유지할 수 있게 됩니다.
균형(Balance)
균형을 나타내는 방법은 '균형 인수(Balance Factor)'라는 것을 이용합니다. 균형 인수는 왼쪽 자식의 높이에서 오른쪽 자식의 높이를 뺀 것으로 균형 인수가 2 이상이거나 -2 이하일 때 균형이 깨졌다고 말합니다.
AVL Tree에서 균형이 깨진 경우의 수는 4가지 뿐입니다.
1 - LL 2 - LR 3 - RL 4 - RR
따라서, AVL Tree를 구현하는 핵심은 이러한 균형이 깨진 트리의 균형을 바로잡아 주는 것입니다.
LL(RR) Rotation
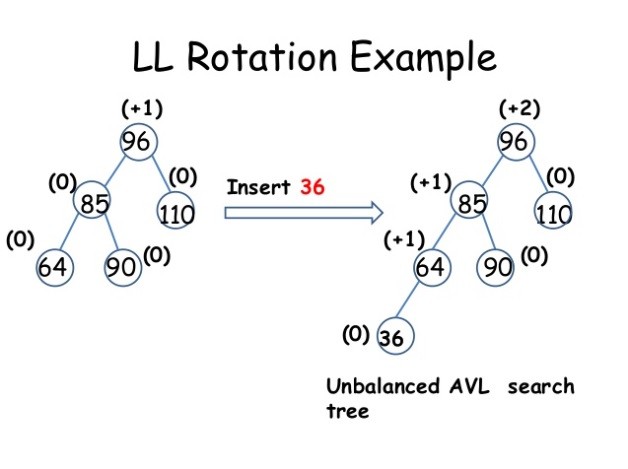
위 그림은 좌측 트리에 36이라는 노드를 추가해 root 노드인 96의 기준에서 left child의 높이와 right child의 높이의 차이, 즉 균형 인수가 2 이기 때문에 균형이 무너진 트리입니다.
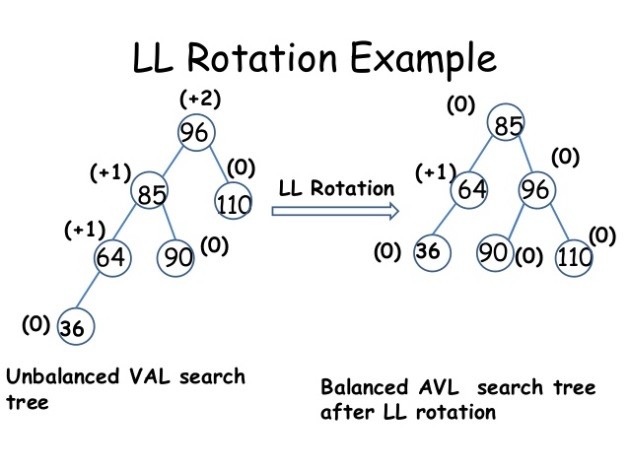
이러한 LL 형태의 Unbalanced Tree에서 균형을 맞추는 방법은 LL Rotation으로, 변형이 일어나야할 노드들 간의 부모 자식 노드연결 구조를 변경해주는 것입니다.
위 그림에서는 96 노드를 A, 85노드를 B라고 했을 때
<pseudo code>
A's left child = B's right child
B's right child = A
LR(RL) Rotation
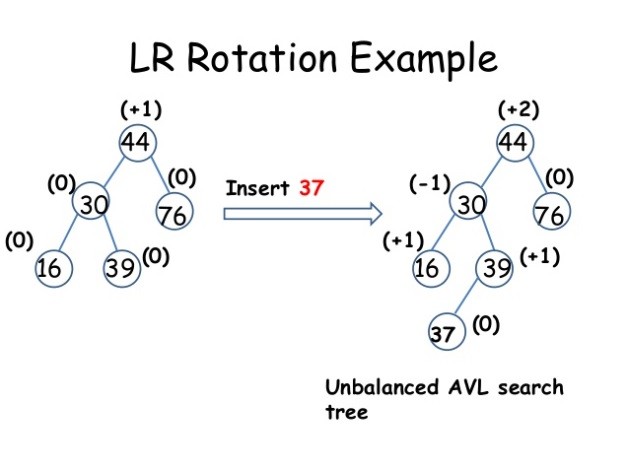
LR(RL) Unbalanced Tree는 지그재그로 불균형한 Tree의 형태입니다. LR(RL)의 경우 LL Rotation으로는 해결이 되지 않고, LL Rotation과 RR Rotation의 합으로 균형을 맞출 수 있습니다.
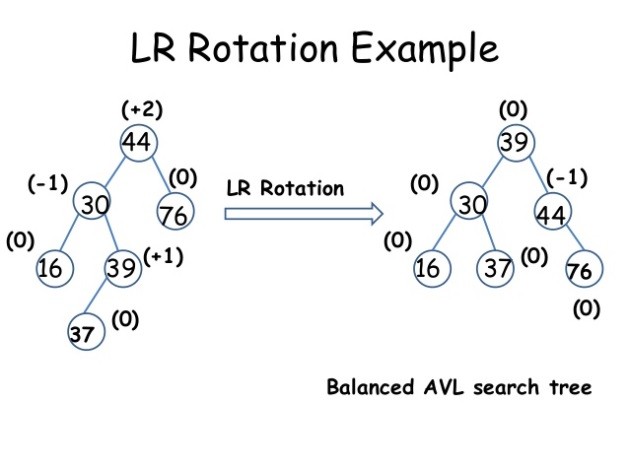
위 그림에서는 30을 기준으로 RR Rotation을 한 뒤 다시 44를 기준으로 LL Rotation 회전을 해준 결과입니다. 즉 쉽게 말해 LR Rotation은 RR Rotation과 LL Rotation을 연달아 해준 것이라고 할 수 있습니다.
(RL Rotation은 LL Rotation 이후 RR Rotation)
<Pseudo code>
A's left child = RR Rotation(B)
LL Rotation(A)
공감(![]() ) 및 댓글은 Ready's tory에 큰 힘!이 됩니다
) 및 댓글은 Ready's tory에 큰 힘!이 됩니다
다음 번에 더더욱 유익한 컨텐츠로 찾아 뵐게요!
* 로그인 없이도 가능하답니다!
내가 주고 싶은 것이 아닌, 당신이 받고 싶은 것을 주겠습니다.
'Algorithm' 카테고리의 다른 글
| [백준 2579번] 계단 오르기 - JAVA (0) | 2019.05.09 |
|---|---|
| [C언어] 최대 연속부분수열의 합 (0) | 2019.02.24 |
| [동적 프로그래밍 예제] 부분집합의 합(C언어) (1) | 2019.01.17 |
| [재귀 알고리즘] 그레이 코드(Gray Code) (0) | 2019.01.15 |
| [재귀 알고리즘] n/m 수분할 (0) | 2019.01.15 |
